🧠 AI with Python – 🐍📈📊 Elbow Method to Find Optimal k

Clustering is a powerful unsupervised learning technique, but one common challenge is deciding the number of clusters (k) to use.

The Elbow Method provides a simple, visual way to determine the optimal k for K-Means clustering.

Why Do We Need the Elbow Method?

• K-Means requires k in advance.
• Too few clusters → underfitting (broad, meaningless groups).
• Too many clusters → overfitting (clusters lose interpretability).
• The Elbow Method strikes a balance by analyzing how clustering performance improves with increasing k.

How It Works

The Elbow Method uses inertia (also called Within-Cluster Sum of Squares, WCSS):

• Inertia measures how tightly grouped the points are within each cluster.
• As k increases, inertia decreases because points are closer to their centroids.
• At some point, adding more clusters yields only marginal improvement → this is the elbow point.

Applying the Elbow Method

We try different values of k and calculate inertia for each.

inertia = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, n_init=10, random_state=42)
    kmeans.fit(X_scaled)
    inertia.append(kmeans.inertia_)

Then we plot inertia against k to visualize the curve.

plt.plot(range(1, 11), inertia, marker="o", linestyle="--")
plt.xlabel("Number of clusters (k)")
plt.ylabel("Inertia (WCSS)")
plt.title("Elbow Method for Optimal k")
plt.show()

Sample Output

The resulting plot looks like this:

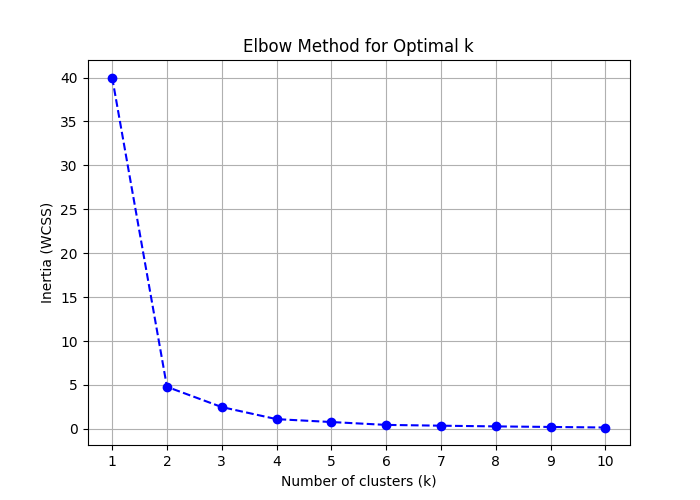
Figure: Elbow Method for Optimal k.

📊 At first, inertia drops steeply. 📊 After a certain k, the curve flattens. 📊 That bend — the elbow point — suggests the optimal number of clusters.

In the demo dataset, the elbow occurs around k = 2 or 3.

Key Takeaways

• The Elbow Method is a quick, intuitive way to estimate k.
• Works best when clusters are well separated.
• Should be combined with other methods (e.g., Silhouette Score) for confirmation.
• Helps avoid overfitting by not adding unnecessary clusters.